Maraigueのメモ倉庫

L2ノルムが決まっているd次元ベクトルvについて、L1ノルムを最大化するには

【補足】

L2ノルムとは簡単にいえば「普通の平面や空間中の距離」（ユークリッド距離。中学校で出てくる、三平方の定理を使って算出される距離）を一般のベクトルについて定義したものである。v = (v₁, v₂, …, v_d) のとき、√(v₁² + v₂² + … + v_d²) で計算するのがL2ノルムである。

L1ノルムとは、「マンハッタン距離」（移動が東西南北にしかできないと考えたときの最小移動経路。詳しくはぐぐって）を一般のベクトルについて定義したものである。v = (v₁, v₂, …, v_d) のとき、|v₁| + |v₂| + … + |v_d| で計算するのがL1ノルムである。

【問題設定】

d次元空間においてL2ノルムがα (α>0) であるようなベクトルのうち、L1ノルムが最大になるのはどのようなときか。

例えば、「2次元空間においてL2ノルムがαであるようなベクトルのうち、L1ノルムが最大のものは？」というのは、図を描けば直感的にわかるだろう（図はα=2）。

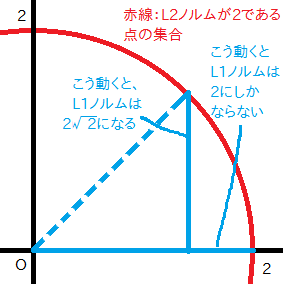
つまり、原点から45度（135度、225度、315度でも同じ）に行く、すなわちベクトルとして(±α/√2, ±α/√2)を選べばよく、そのときのL1ノルムは α×√2 となる。

これは一般化すれば、d次元空間においてL2ノルムがαであるようなベクトルのうち、L1ノルムが最大のものは、おそらく (±α/√d, ±α/√d, …, ±α/√d)（そのときのL1ノルムは α・√d）になるのだろうけど、その証明がすぐに思いつかなかったのである。

【解き方の方針】

ふと「ラグランジュの未定乗数法」を使えば解けるとわかったので、それで解いた。
ラグランジュの未定乗数法とは簡単にいえば、条件付きの多変数の最大化/最小化を行うときに用いられる計算である。

ベクトルvを引数に取り実数一つを返す関数 f(v) は、vに制限がなければ、vが以下の条件を満たすときに極大あるいは極小になる。

∂f(v)/∂v₁ = 0, ∂f(v)/∂v₂ = 0, …, ∂f(v)/∂v_d = 0

一方でラグランジュの未定乗数法では、vに制限を加えて「f(v)が、g(v)=0という条件を満たす中で極大/極小になる」というものを考える。その条件は、F(v) = f(v) - λg(v) とおいたとき、vが以下の条件を満たすときに極大あるいは極小になるというものである。

g(v)=0, ∂F(v)/∂v₁ = 0, ∂F(v)/∂v₂ = 0, …, ∂F(v)/∂v_d = 0

【答え】

結論から言うと、上記の予想「L1ノルムを最大にするベクトルvは v = (±α/√d, ±α/√d, …, ±α/√d) で、そのときのL1ノルムは α・√d」は正しい。

上記のラグランジュの未定乗数法における条件において、

• f(v) = |v₁| + |v₂| + … + |v_d|
• g(v) = v₁² + v₂² + … + v_d² - α²

とする。g(v)については「L2ノルムがαである」ことを表現する代わりに、「L2ノルムの2乗がα²である」としている（平方根を含んだままでは計算しにくいため）。

これを踏まえて ∂F(v)/∂v_i (i ∈ {1, 2, …, d}) を計算すると

• v_i > 0 のとき、∂F(v)/∂v_i = 1 - 2λ・v_i
• v_i < 0 のとき、∂F(v)/∂v_i = -1 - 2λ・v_i
  
• v_i = 0 のとき、微分不能（別途検討する→補足2）

となるので、v_i = 0 の場合を除くと、∂F(v)/∂v_i = 0 ⇒ |v_i| = 1/2λ が極値となる条件となることがわかる。これを g(v) = 0 に当てはめると、(1/2λ)² + (1/2λ)² + … + (1/2λ)² - α² = 0 より d/(4λ²) = α², つまり 1/2λ = α/√d となる。すなわち、|v_i| = α/√d がL1ノルムを最大にする条件であり、そのときのL1ノルムは α・√d である。（終）
（本当はこれは極値でしかなく、極大/極小の判定や最大であることの証明も必要である→補足1）

（補足1）

極大/極小の判定には本来であれば、∂² F(v)/∂v_i∂v_j をすべてのi, jの組み合わせに対して行わないとならない。しかしこの場合は不要であって、単に ∂² F(v)/∂v_i∂v_i が計算できればよい。なぜなら式の形より、i≠j のとき ∂² F(v)/∂v_i∂v_j は明らかに0になるからである。

さてこれを計算すると、v_i≠0のとき、∂² F(v)/∂v_i∂v_i = -2λ となる。先述の計算で「|v_i| = 1/2λ」という条件があったので、-2λは負の数である。∂² F(v)/∂v_i∂v_i がすべての i について同一の負の数であって、かつ i≠j のとき ∂² F(v)/∂v_i∂v = 0 のときは、その点vではF(v)は極大値となることが知られている。（より詳しくは「ヘッセ行列」というものを利用して定式化できる。多変数関数の極値判定とヘッセ行列 | 高校数学の美しい物語）

極大値がこれらの点しかなく、かつf(v)の値は有界なので、これらは最大値である。

（補足2）

もし v_i = 0 となるような i が存在する（すなわち、ベクトルの要素の少なくとも一つが0である）ときにL1ノルムが最大になりえないことを確かめ、証明を完了する。

v_i = 0となる i がk個存在するとする（0 < k < d）。このとき、残る d - k 個の数について、「d-k 次元ベクトルのL2ノルムが α であるという条件のもとで、L1ノルムを最大化する」ことを考えると、そのときのL1ノルムは α・√(d-k) となる。よってこちらのほうがα・√dよりも小さいので、v_i = 0 となるような i が存在するときにL1ノルムは最大にはなりえない。

（循環論法にも見えるが、dが小さい側から順番に証明して数学的帰納法を使っていると考えればよい。d=2のときはk=1しかないので直接計算すればよい。）