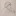Today’s glossary provoked by Michael Spivak.

Below I’ve drawn two vector spaces connected by a linear homomorphism ƒ, plus a linear functional λ going to ℝ. After seeing these pictures I hope it’s easier to understand how the pullback ƒ* works.
Here’s one of the main pictures for flavour:
Also, you can probably just skim the pictures and get the point (especially the Number Field one and the final one). That’s the fastest way to read this post.
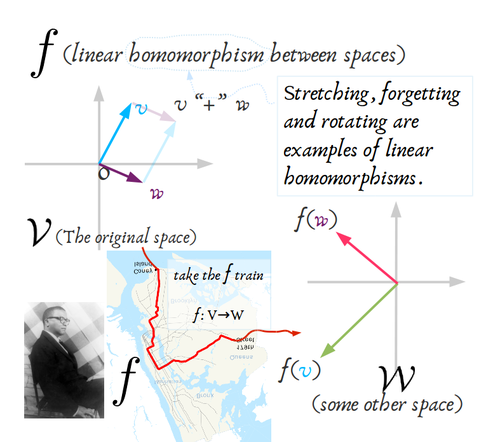
Start with an abstract 𝓥ector space.
I’ll do some violence because I’ll need coordinates in a minute.

The simplest way to think about a linear function, in 1-D, is as continued addition of some constant. Say the constant were 4, then linear would be +4+4+4+4+4+4+4+.... If the constant were m then linear would be +m+m+m+m+m+m+m+m+... “x” times, or y=mx in the usual jargon.

Linearity is a strong enough condition that I can infer everything that happens on my “horizontal number line” (the first dimension I violently imposed). It has to be +4+4+4+..., adding that same constant every tick right.

Linearity–and weaker conditions like homomorphism–fix zero. The zero of the domain has to map onto the zero of the codomain. So you always know linear subspaces are “centred”, they have to contain zero at least.

Since I’m doing 2-D, I need to make up another constant for what the λ functional does in my “vertical direction”. To be really interesting I chose +1+1+1+1+1+1+.... I can make the arithmetic really easy on myself. I don’t have to work in some skewy, wonky basis. Instead, it’s necessarily possible to choose directions that will “work like” independent horizontal and vertical, even coming from an abstract vector space like the parameters for spline-based functions modelling heart arrhythmia. So I’m making all my constants positive and aligning the axes perpendicularly.
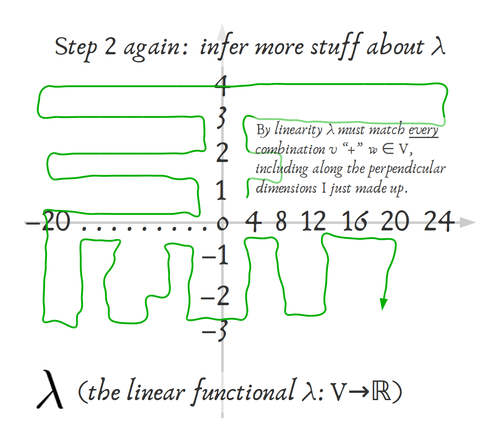
Now, again because of linearity, λ is very limited in what it can do. Remember homomorphisms ƒ always do ƒ(→+↑) = ƒ(→)+ƒ(↑). (Here → and ↑ stand for “vertical” and “horizontal” movement–as I violently defined them–in the initial space 𝓥.) So I can just maze through or Sudoku through all the points in 𝓥 and figure out what λ has to do there, now that I’ve chosen vertical constant to be +1+1+1+1+1+.... and horizontal constant to be +4+4+4+4+4+.....

So if over → is +4 and up ↑ is +1, then over & up →↑ = +5 = up & over ↑→. By homomorphic-ness of ƒ.

I can continue to maze my way around, figuring out what λ has to do since I already chose the only two constants there are to choose for λ.
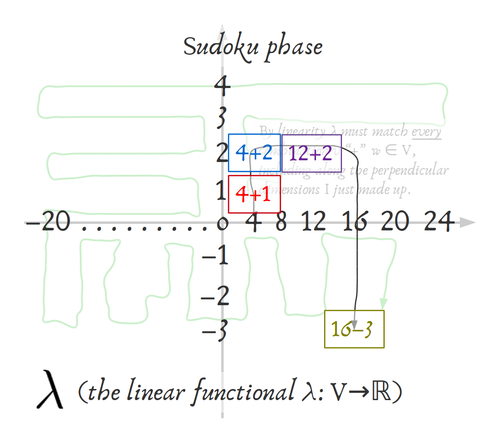
This is just like a sudoku! Except not painfully boring. I line up two thingies and they make a thingy.

Yes! Take that, tube puzzles.

I’ll just evaluate those….

…and remove the ornamentation now that you get the point…

You can see it’s a proper number field! (The most familiar number fields, if you watch TV, are the weather maps

but of course nowadays we do “heatmaps” of various things that are not heat:

By “number field” I just mean to each region or point, is assigned a number ∈ℝ.

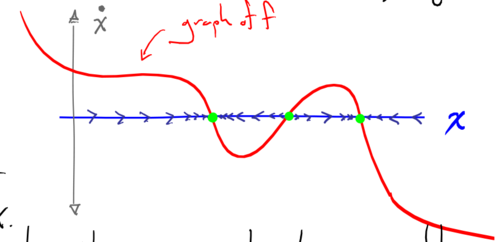
This is a linear 2-D number field, whereas Ghrist drew us a nice picture of a smooth 1-D number field (“differential one-form”), interpreted with relevance to dynamical systems and their equilibria.
If you cared to, you could compute some stuff about this number field. Like the distance you have to go, in what direction, before the level set increments up. Or the slope of the level sets. For instance look at one of the 11’s and try to find the other 11 by looking at the pattern of the other equi-coloured pairs.

If you can see through the colour barf, then you’ll notice the level sets are all straight and all march with even pace.
This derives from the linearity and homomorphic-ness of λ.

Now that’s λ sorted. What was the original question? Oh yeah, Spivvy.

He started us off with three things: 𝓥, ƒ, and λ.

I assumed you knew 𝓥 and only talked about λ, some linear N→1-dimensional function. I’ll do a bit about ƒ, the 3rd ingredient–a homomorphism of spaces–as well.
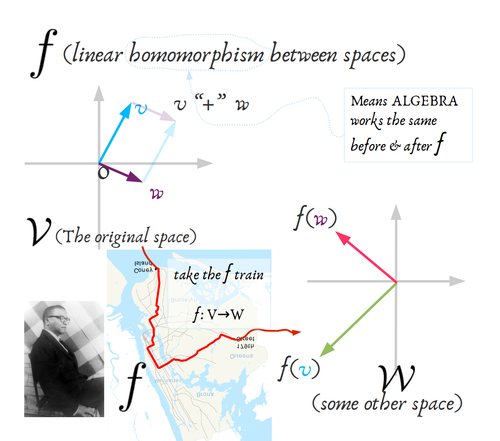
Homomorphisms work for “going the long way” because they preserve algebra.

All of the usual matrices preserve linear structure. Meaning we can do convenient things like pretend (as I did above) that I can decompose an arbitrary abstract vector-space into independent pieces: because that goal is just a matrix transform away. Since matrix transforms preserve all of the properties I’m using (linearity), I just need to keep a spare gauge in my pocket, knowing I can spend it if necessary to enter the annoying world of actual numbers to work something out. But, knowing that I could if I wanted to, I’ll dispense with the actual work whenever possible.
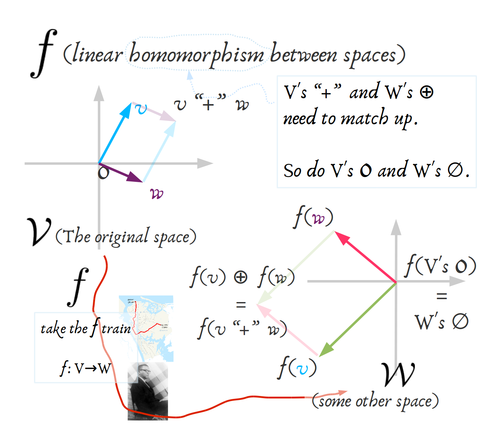
There’s something about “data types” here. In the abstract vector spaces 𝓥 and ƒ(𝓥) = 𝓦, we allowed ourselves quite a bit of freedom. In fact that’s why this is interesting: because 𝓥 and 𝓦 are general enough to represent something interesting, not just the triangles and squares and circles and numbers of grade-school mathematics.
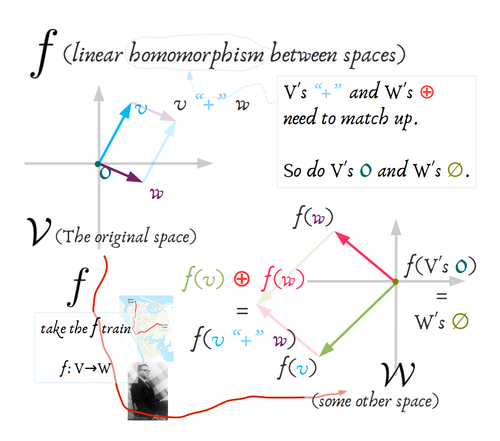
What that means is that I allowed myself to call 𝓥 and 𝓦 vector spaces, so long as I could come up with some properly commuting, distributing, zero-and-one-having pair of binary operations. But that means that 𝓥’s “plus” and 𝓦’s “plus” might not be the same! Since both are relatively free concepts on their own. But as a homomorphism, ƒ still needs to match them up.
So I’ve tried to indicate the situation with colour barf above. Does that work for you??? 𝓥’s stuff gets purplish/bluish colours and 𝓦’s stuff gets an equally tasteful, yet distinctive, pink/green/brown palette.
The harmless-looking algebra of ƒ(v+w) = ƒ(v) + ƒ(w) is not trivial at all! So I try to substitute something like ƒ(v+w) = ƒ(v) ⊕ ƒ(w) to emphasise that these are not the same plus signs. They’re not operating on the same datatype: + operates on 𝓥’s things and ⊕ operates on 𝓦’s things. It could be something like + operating on frequency bands and ⊕ operating on circuit superpositions–freq-bands and circuits aren’t even the same kind of thing.
(Also 𝓥’s “zero” and 𝓦’s “zero” aren’t the same. Like a null circuit ≠ a null set ≠ a null operator ≠ a null trade ≠ a null wave … they all do nothing, but they do it to different kinds of things.)
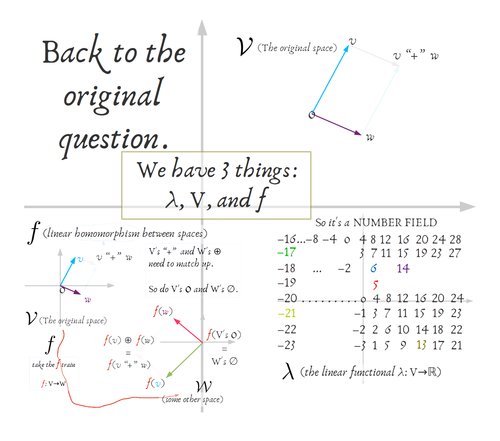
So Spivak started us with essentially a diagram chase:

The simplest homomorphism ƒ I can think of would be rotating the basis,

so let’s do that one.

In that case there’s an “obvious” way to put λ and the rotation ƒ together: just rotate the number field.
You could transform the number field by any old matrix as well – I just didn’t want to draw those ones. But if you were plotting a linear heatmap in R then matrix-transformations of that heatmap would be easy enough to do and you could see the precomposition of λ with ƒ that way.
Now, that’s not explaining the pullback ƒ*, but the “precomposition” idea is what I guess you need to understand that passage in Spivak. Here it is again.